Monday, 18 June 2012
In:
Reflection
DAY 6 (19/06/2012)
Ini adalah kelas terakhir kami untuk subjek TIE dan pembentangan fasa kedua yang masih berbaki 8 kumpulan. Bermakna ni lah kali terakhir berjumpa dengan Encik Azrul


Selepas menempuhi minggu yang begitu mencabar untuk menyiapkan semua tugasan yang diberikan (sampai mata pun da jadi macam panda)



Kami berharap kami semua akan memperoleh markah yang cemerlang dalam subjek ini dan semua subjek-subjek yang lain.
Kami amat sedih untuk meninggalkan kawan-kawan, pensyarah dan UIAM kerana ini merupakan sesi terakhir kami belajar DipEd di sini. Walaupun agak sedih untuk meninggalkan kelas ni tapi apakan daya.




Harapan kami, selepas tamat DipEd ini, kami akan lebih berpengetahuan dan mengajar dengan lebih cemerlang untuk memajukan anak bangsa kami.
Sekian sahaja untuk masa ini. Kami akhiri reflection ini dengan serangkap pantun
Kalau ada sumur di ladang,
Boleh kami menumpang mandi,
Kalau ada umur yang panjang,
Boleh kita berjumpa lagi....

Properties of the Complex Set
The set of complex numbers is denoted 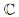 . Just like any other number set there are rules of operation.
. Just like any other number set there are rules of operation.
The sum and difference of complex numbers is defined by adding or subtracting their real components ie: 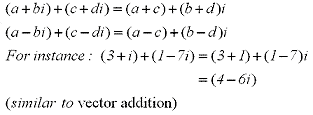 The communitive and distributive properties hold for the product of complex numbers ie:
The communitive and distributive properties hold for the product of complex numbers ie:
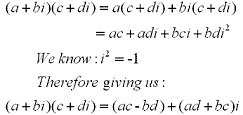 When dividing two complex numbers you are basically rationalizing the denominator of a rational expression. If we have a complex number defined as z =a+bi then the conjuate would be
When dividing two complex numbers you are basically rationalizing the denominator of a rational expression. If we have a complex number defined as z =a+bi then the conjuate would be 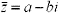 . See the following example:
. See the following example:Example:
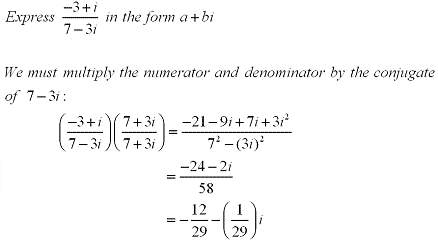
Conjugates
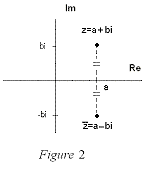
The geometric inperpretation of a complex conjugate is the reflection along the real axis. This can be seen in the figure below where z = a+bi is a complex number. Listed below are also several properties of conjugates.
Properties:
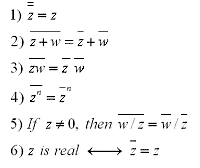
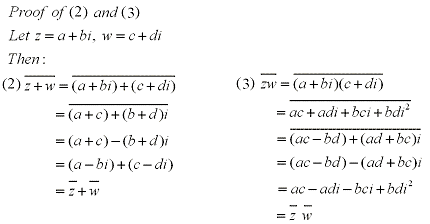
credit to :
http://algebra.nipissingu.ca/tutorials/complex_numbers.html
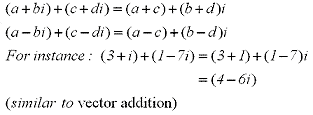
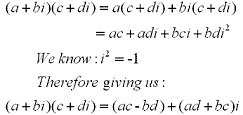
When dividing two complex numbers you are basically rationalizing the denominator of a rational expression. If we have a complex number defined as z =a+bi then the conjuate would be 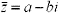 . See the following example:
. See the following example:
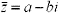 . See the following example:
. See the following example:Example:
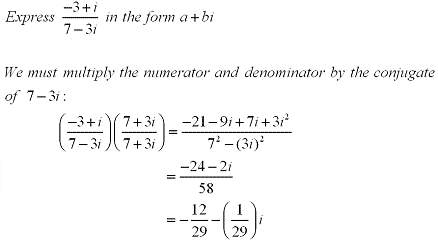
Conjugates
The geometric inperpretation of a complex conjugate is the reflection along the real axis. This can be seen in the figure below where z = a+bi is a complex number. Listed below are also several properties of conjugates.
Properties:
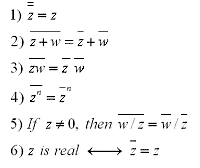

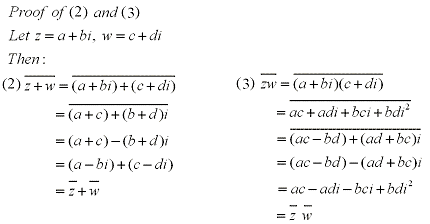
credit to :
http://algebra.nipissingu.ca/tutorials/complex_numbers.html
Properties:
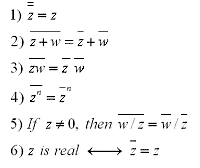

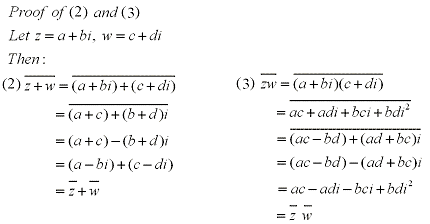
credit to :
http://algebra.nipissingu.ca/tutorials/complex_numbers.html
Complex Numbers
A complex number is made up of both real and imaginary components. It can be represented by an expression of the form (a+bi), where a and b are real numbers and i is imaginary. When defining i we say that i = 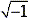 . Then we can think of i2 as -1. In general, if c is any positive number, we would write:
. Then we can think of i2 as -1. In general, if c is any positive number, we would write: 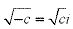 .If we have a complex number z, where z=a+bi then a would be the real
.If we have a complex number z, where z=a+bi then a would be the real 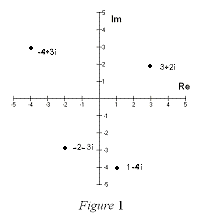 component (denoted: Re z) and b would represent the imaginary component of z (denoted Im z). Thus the real component of z=4+3i is 4 and the imaginary component would be 3. From this, it is obvious that two complex numbers (a+bi) and (c+di) are equal if and only if a=c and b=d, that is, the real and imaginary components are equal.The complex number (a+bi) can also be represented by the ordered pair (a,b) and plotted on a special plane called the complex plane or the Argand Plane. On the Argand Plane the horizontal axis is called the real axis and the vertical axis is called the imaginary axis. This is shown in Figure 1 on the right:
component (denoted: Re z) and b would represent the imaginary component of z (denoted Im z). Thus the real component of z=4+3i is 4 and the imaginary component would be 3. From this, it is obvious that two complex numbers (a+bi) and (c+di) are equal if and only if a=c and b=d, that is, the real and imaginary components are equal.The complex number (a+bi) can also be represented by the ordered pair (a,b) and plotted on a special plane called the complex plane or the Argand Plane. On the Argand Plane the horizontal axis is called the real axis and the vertical axis is called the imaginary axis. This is shown in Figure 1 on the right:
credit to :
http://algebra.nipissingu.ca/tutorials/complex_numbers.html
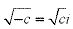 .
. component (denoted: Re z) and b would represent the imaginary component of z (denoted Im z). Thus the real component of z=4+3i is 4 and the imaginary component would be 3. From this, it is obvious that two complex numbers (a+bi) and (c+di) are equal if and only if a=c and b=d, that is, the real and imaginary components are equal.
component (denoted: Re z) and b would represent the imaginary component of z (denoted Im z). Thus the real component of z=4+3i is 4 and the imaginary component would be 3. From this, it is obvious that two complex numbers (a+bi) and (c+di) are equal if and only if a=c and b=d, that is, the real and imaginary components are equal.credit to :
http://algebra.nipissingu.ca/tutorials/complex_numbers.html
DAY 5 (15/06/2012)
Kami merupakan kumpulan yang pertama tiba ke kelas kerana semangat yang berkobar-kobar untuk pembentangan pada hari ini. Setelah melakukan semua persiapan untuk memastikan pembentangan kami berjalan dengan lancar, kami menunggu En. Azrul tiba ke kelas. Alhamdullilah, pembentangan kami berjalan seperti apa yang telah dirancangkan walaupun agak tergesa-gesa menyiapkan tugasan yang diberikan sehingga mata kami semua menjadi seperti "Panda".

Kami rasa telah melakukan yang terbaik dan telah mematuhi semua ciri-ciri dalam Gagne Nine Events of Instruction (mintak2 En Azrul bagi markah lebih~bagi markah best2 ok!). Setelah selesai semua kumpulan membuat pembentangan kami dibenarkan bersurai.
Setelah selesai semua kumpulan membuat pembentangan kami dibenarkan bersurai.

Kami rasa telah melakukan yang terbaik dan telah mematuhi semua ciri-ciri dalam Gagne Nine Events of Instruction (mintak2 En Azrul bagi markah lebih~bagi markah best2 ok!).
 Setelah selesai semua kumpulan membuat pembentangan kami dibenarkan bersurai.
Setelah selesai semua kumpulan membuat pembentangan kami dibenarkan bersurai.
Sunday, 17 June 2012
In:
Reflection
DAY 4 (14/06/2012)
Encik Azrul menerangkan tentang panduan membuat powerpoint bagi pembentangan kami. Pembentangan akan merangkumi 55% markah dan ia mestilah merangkumi Gagne Nine Events of Instructions. Kami memilih tajuk yang telah dibentangkan pada hari pertama iaitu Imaginary Numbers.
Kami diminta memilih huruf dihadapan untuk menentukan giliran pembantangan pada perjumpaan ke-5 dan ke-6. Memandangkan kami begitu bertuah, kami telah memilih huruf "D" yang menjurus kepada giliran yang pertama..(HOREYYYY!!!)

Pada awalnya, kami agak terkejut,  tapi menerima cabaran itu dengan optimis dan positif. Selepas itu, En Azrul memberi masa kepada kami untuk menyiapkan powerpoint. Kami sempat mencari dan menyusun bahan mengikut Gagne Nine Events of Instruction dan akan menyiapkan pada malam itu. Dengan kesungguhan kami berlima, akhirnya kami berjaya juga buat sehingga jam 2 pagi.
tapi menerima cabaran itu dengan optimis dan positif. Selepas itu, En Azrul memberi masa kepada kami untuk menyiapkan powerpoint. Kami sempat mencari dan menyusun bahan mengikut Gagne Nine Events of Instruction dan akan menyiapkan pada malam itu. Dengan kesungguhan kami berlima, akhirnya kami berjaya juga buat sehingga jam 2 pagi. 
 tapi menerima cabaran itu dengan optimis dan positif. Selepas itu, En Azrul memberi masa kepada kami untuk menyiapkan powerpoint. Kami sempat mencari dan menyusun bahan mengikut Gagne Nine Events of Instruction dan akan menyiapkan pada malam itu. Dengan kesungguhan kami berlima, akhirnya kami berjaya juga buat sehingga jam 2 pagi.
tapi menerima cabaran itu dengan optimis dan positif. Selepas itu, En Azrul memberi masa kepada kami untuk menyiapkan powerpoint. Kami sempat mencari dan menyusun bahan mengikut Gagne Nine Events of Instruction dan akan menyiapkan pada malam itu. Dengan kesungguhan kami berlima, akhirnya kami berjaya juga buat sehingga jam 2 pagi. 
DAY 3 (13/06/2012)
Pada permulaan kelas, kami menjalani peperiksaan midterm dengan jayanya (walaupun ada silap sedikit, tapi menurut En. Azrul, purata markat kami 17, terima kasih En Azrul). Selepas selesai peperiksaan, kami menanda kertas sesama sendiri. tidak sampai satu jam, semua proses telah selesai. (tak sia-sia study malam sebelum tu) 

Selepas selesai midterm, kami diberi masa untuk menyiapkan dan menambah baik blog. kami berkesempatan untuk memuat naik beberapa nota berkenaan tajuk Gradient.
DAY 2 (12/06/2012)
Encik Azrul menerangkan topik yang akan di soal dalam peperiksaan pertengahan semester yang akan dibuat pada perjumpaah ketiga (Rabu) iaitu keesokkan harinya. walaupun pada masa yang begitu singkat, kami tetap komited untuk mempelajari subjek ini dengan keyakinan dan ketabahan kerana En Azrul begitu bersungguh-sungguh memberi penerangan kepada kami semua (ini betul-betul, bukan mengampu).
Peperiksaan midterm merangkumi topik Learning Theories and Models, Gagne nine events of instructions, Instructional Media. Kami telah dimaklumkan lebih awal bentuk soalan dan tips-tips penting untuk menjawab.
selepas selesai sesi pengajaran, kami diberi latihan melalui forum di e-celpad. terdapat 14 soalan klon (macam SPM tu) sebagai latihan.
DAY 1 (11/06/2012)
Kami diperkenalkan dengan portal e-celpad untuk membantu pembelajaran dan memudahkan komunikasi antara kami dan Pensyarah serta bertukar maklumat dengan rakan yang lain. Selain itu, terdapat juga maklumat berkenaan peratusan penilaian yang terbahagi kepada 3 iaitu, Midtem (20 marks), Production of Instructional Media (55 marks) dan Blog for e-portfolio (25 marks)~Chaiyo!! 

Kami diminta untuk membuka akaun di http://myenglish.e-celpad.com/login/index.php secara individu. Pada awalnya, kami bertiga berkongsi akaun yang sama tetapi sebelum kelas berakhir, kami sempat untuk membuat akaun secara berasingan.
Encik Azrul menerangkan topik Gagne nine event of Instructions. Kami juga membuka akaun di blogspot dan memilih tajuk Gradient of straight line, Integration dan Differentiation yang berfokus kepada topik dalam subjek matematik untuk pelajar IKM.
Kami juga membuat penerangan ringkas menggunakan Gagne nine event of Instructions dan kami memilih topik Imaginary Numbers sebagai pembentangan kumpulan kami.
Rules of Integration
Our proofs will involve searching for a function F(x) whose derivative is 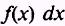 .
.
The integral of a differential of a function is the function plus a constant.
PROOF: If
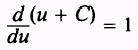
then
and
EXAMPLE. Evaluate the integral
SOLUTION: By Rule 1, we have
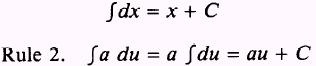
A constant may be moved across the integral sign. NOTE: A variable may NOT be moved across the integral sign.
PROOF: If
then
and
EXAMPLE: Evaluate the integral
SOLUTION: By Rule 2,
and by Rule 1,
therefore,
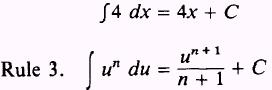
The integral of 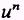 du may be obtained by adding 1 to the exponent and then dividing by this new exponent. NOTE: If n is minus 1, this rule is not valid and another method must be used.
du may be obtained by adding 1 to the exponent and then dividing by this new exponent. NOTE: If n is minus 1, this rule is not valid and another method must be used.
PROOF.- If
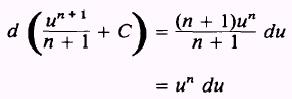
then
EXAMPLE: Evaluate the integral
SOLUTION: By Rule 3,
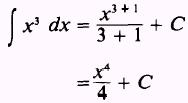
EXAMPLE: Evaluate the integral
SOLUTION: First write the integral
as
Then, by Rule 2,
and by Rule 3,
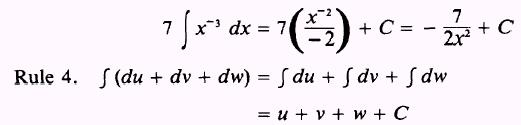
The integral of a sum is equal to the sum of the integrals.
PROOF: If
PROOF: If
then
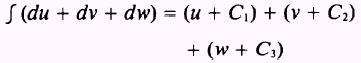
such that
where
EXAMPLE: Evaluate the integral
SOLUTION: We will not combine 2x and -5x.
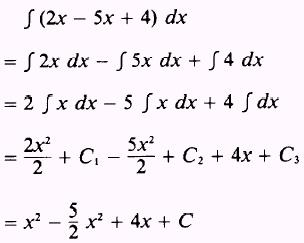
where C is the sum of 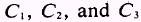 .
.
EXAMPLE: Evaluate the integral
SOLUTION:
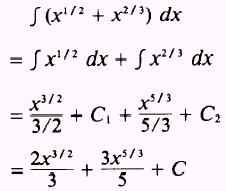
Now we will discuss the evaluation of the constant of integration.
If we are to find the equation of a curve whose first derivative is 2 times the independent variable x, we may write
or
We may obtain the desired equation for the curve by integrating the expression for dy; that is, by integrating both sides of equation (1). If
then,
But, since
and
then
We have obtained only a general equation of the curve because a different curve results for each value we assign to C. This is shown in figure 6-7. If we specify that
x=0
And
y=6
we may obtain a specific value for C and hence a particular curve.
Suppose that
then,
or
C=6
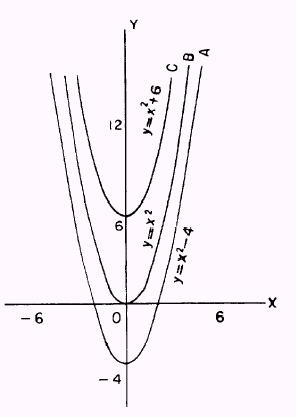
Figure 6-7.-Family of curves.
By substituting the value 6 into the general equation, we find that the equation for the particular curve is
which is curve C of figure 6-7.
The values for x and y will determine the value for C and also determine the particular curve of the family of curves.
In figure 6-7, curve A has a constant equal to - 4, curve B has a constant equal to 0, and curve C has a constant equal to 6.
EXAMPLE: Find the equation of the curve if its first derivative is 6 times the independent variable, y equals 2, and x equals 0.
SOLUTION. We may write
or
such that,
Solving for C when
x=0
and
y=2
We have
or
C=2
so that the equation of the curve is
Check out more notes here
http://people.hofstra.edu/stefan_waner/realworld/tutorials4/frames6_1.html
Subscribe to:
Comments (Atom)




