Monday, 18 June 2012
In:
Complex Numbers
Complex Numbers
A complex number is made up of both real and imaginary components. It can be represented by an expression of the form (a+bi), where a and b are real numbers and i is imaginary. When defining i we say that i = 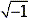 . Then we can think of i2 as -1. In general, if c is any positive number, we would write:
. Then we can think of i2 as -1. In general, if c is any positive number, we would write: 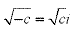 .If we have a complex number z, where z=a+bi then a would be the real
.If we have a complex number z, where z=a+bi then a would be the real 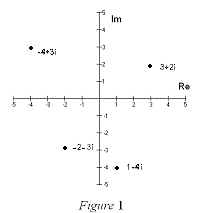 component (denoted: Re z) and b would represent the imaginary component of z (denoted Im z). Thus the real component of z=4+3i is 4 and the imaginary component would be 3. From this, it is obvious that two complex numbers (a+bi) and (c+di) are equal if and only if a=c and b=d, that is, the real and imaginary components are equal.The complex number (a+bi) can also be represented by the ordered pair (a,b) and plotted on a special plane called the complex plane or the Argand Plane. On the Argand Plane the horizontal axis is called the real axis and the vertical axis is called the imaginary axis. This is shown in Figure 1 on the right:
component (denoted: Re z) and b would represent the imaginary component of z (denoted Im z). Thus the real component of z=4+3i is 4 and the imaginary component would be 3. From this, it is obvious that two complex numbers (a+bi) and (c+di) are equal if and only if a=c and b=d, that is, the real and imaginary components are equal.The complex number (a+bi) can also be represented by the ordered pair (a,b) and plotted on a special plane called the complex plane or the Argand Plane. On the Argand Plane the horizontal axis is called the real axis and the vertical axis is called the imaginary axis. This is shown in Figure 1 on the right:
credit to :
http://algebra.nipissingu.ca/tutorials/complex_numbers.html
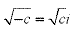 .
. component (denoted: Re z) and b would represent the imaginary component of z (denoted Im z). Thus the real component of z=4+3i is 4 and the imaginary component would be 3. From this, it is obvious that two complex numbers (a+bi) and (c+di) are equal if and only if a=c and b=d, that is, the real and imaginary components are equal.
component (denoted: Re z) and b would represent the imaginary component of z (denoted Im z). Thus the real component of z=4+3i is 4 and the imaginary component would be 3. From this, it is obvious that two complex numbers (a+bi) and (c+di) are equal if and only if a=c and b=d, that is, the real and imaginary components are equal.credit to :
http://algebra.nipissingu.ca/tutorials/complex_numbers.html
Subscribe to:
Post Comments (Atom)


0 comments:
Post a Comment