Monday, 18 June 2012
In:
Complex Numbers
Properties of the Complex Set
The set of complex numbers is denoted 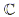 . Just like any other number set there are rules of operation.
. Just like any other number set there are rules of operation.
The sum and difference of complex numbers is defined by adding or subtracting their real components ie: 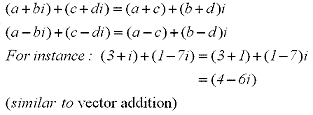 The communitive and distributive properties hold for the product of complex numbers ie:
The communitive and distributive properties hold for the product of complex numbers ie:
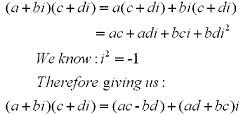 When dividing two complex numbers you are basically rationalizing the denominator of a rational expression. If we have a complex number defined as z =a+bi then the conjuate would be
When dividing two complex numbers you are basically rationalizing the denominator of a rational expression. If we have a complex number defined as z =a+bi then the conjuate would be 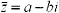 . See the following example:
. See the following example:Example:
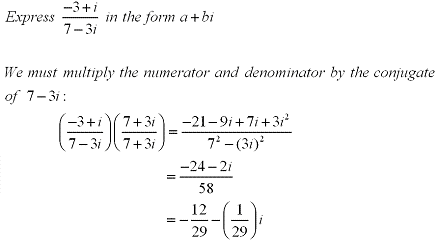
Conjugates
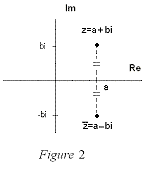
The geometric inperpretation of a complex conjugate is the reflection along the real axis. This can be seen in the figure below where z = a+bi is a complex number. Listed below are also several properties of conjugates.
Properties:
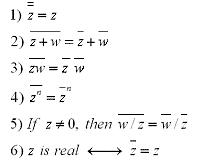
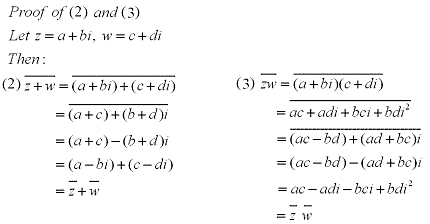
credit to :
http://algebra.nipissingu.ca/tutorials/complex_numbers.html
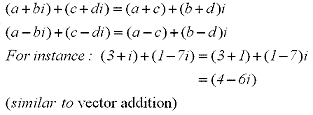
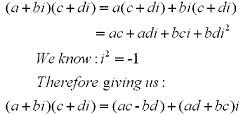
When dividing two complex numbers you are basically rationalizing the denominator of a rational expression. If we have a complex number defined as z =a+bi then the conjuate would be 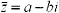 . See the following example:
. See the following example:
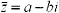 . See the following example:
. See the following example:Example:
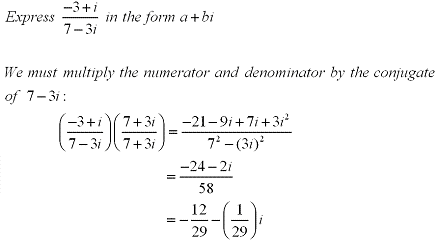
Conjugates
The geometric inperpretation of a complex conjugate is the reflection along the real axis. This can be seen in the figure below where z = a+bi is a complex number. Listed below are also several properties of conjugates.
Properties:
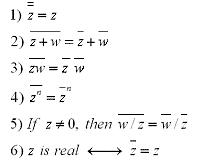

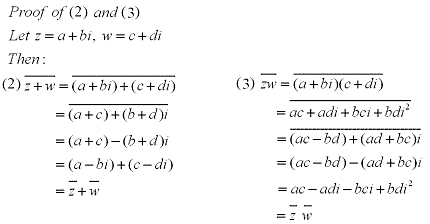
credit to :
http://algebra.nipissingu.ca/tutorials/complex_numbers.html
Properties:
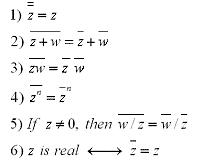

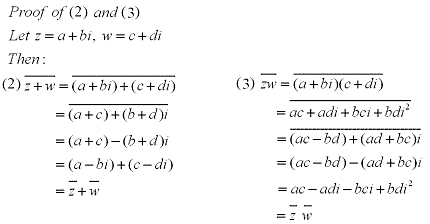
credit to :
http://algebra.nipissingu.ca/tutorials/complex_numbers.html
Subscribe to:
Post Comments (Atom)


0 comments:
Post a Comment