Rules of Integration

Our proofs will involve searching for a function F(x) whose derivative is .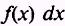

The integral of a differential of a function is the function plus a constant.

PROOF: If

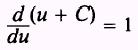
then

and

EXAMPLE. Evaluate the integral

SOLUTION: By Rule 1, we have

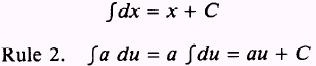
A constant may be moved across the integral sign. NOTE: A variable may NOT be moved across the integral sign.

PROOF: If

then

and

EXAMPLE: Evaluate the integral

SOLUTION: By Rule 2,

and by Rule 1,

therefore,

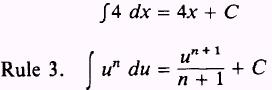
The integral of 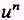du may be obtained by adding 1 to the ex­ponent and then dividing by this new exponent. NOTE: If n is minus 1, this rule is not valid and another method must be used.

PROOF.- If

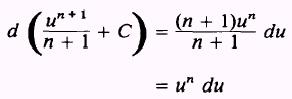
then

EXAMPLE: Evaluate the integral

SOLUTION: By Rule 3,

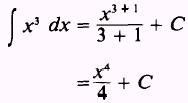
EXAMPLE: Evaluate the integral

SOLUTION: First write the integral

as

Then, by Rule 2,

and by Rule 3,

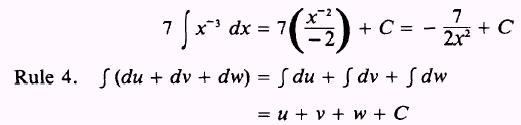
The integral of a sum is equal to the sum of the integrals.
PROOF: If

then

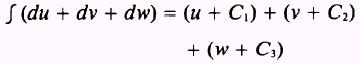
such that

where

EXAMPLE: Evaluate the integral

SOLUTION: We will not combine 2x and -5x.

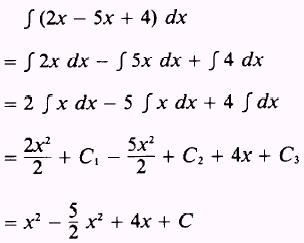
where C is the sum of .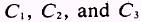

EXAMPLE: Evaluate the integral

SOLUTION:

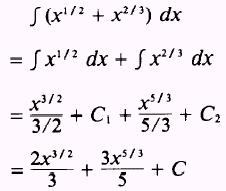
Now we will discuss the evaluation of the constant of integration.

If we are to find the equation of a curve whose first derivative is 2 times the independent variable x, we may write

or

We may obtain the desired equation for the curve by integrating the expression for dy; that is, by integrating both sides of equa­tion (1). If

then,

But, since

and

then

We have obtained only a general equation of the curve because a different curve results for each value we assign to C. This is shown in figure 6-7. If we specify that

x=0

And

y=6

we may obtain a specific value for C and hence a par­ticular curve.

Suppose that

then,

or

C=6

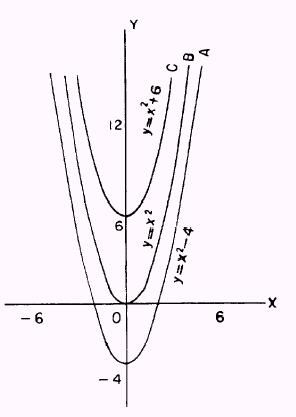
Figure 6-7.-Family of curves.

By substituting the value 6 into the general equation, we find that the equation for the particular curve is

which is curve C of figure 6-7.

The values for x and y will determine the value for C and also determine the particular curve of the family of curves.

In figure 6-7, curve A has a constant equal to - 4, curve B has a constant equal to 0, and curve C has a constant equal to 6.

EXAMPLE: Find the equation of the curve if its first derivative is 6 times the independent variable, y equals 2, and x equals 0.

SOLUTION. We may write

or

such that,

Solving for C when

x=0

and

y=2

We have

or

C=2

so that the equation of the curve is

 

Check out more notes here
http://people.hofstra.edu/stefan_waner/realworld/tutorials4/frames6_1.html